Previous Home Contents Next

Chapter 22: First encounters of an Aldor novice

22.1 Overview

22.2 First vignette: a modified factorial function

22.3 Second vignette: the Lambert W function

22.4 Third vignette: binary doubling

22.5 Fourth vignette: compact finite differences

22.6 Fifth vignette: rounded rationals

22.7 Retrospective

22.1 : Overview

This chapter is a report of my first experiences with Aldor. The programs that I wrote are disjointed and (mostly) unrelated. They will be presented as a series of vignettes which can be read independently, though they will be given in historical order.

I first learned to program in ALGOL-W, which was rather like Pascal (only better). Subsequently, I have used lots of ``blockish'' languages like Fortran. My most usual languages for programming at the moment are Maple, MATLAB, Derive, and occasionally RPL, the language for the Hewlett-Packard 48 calculators. I wrote my last LISP program more than 15 years ago. I have never programmed in C, ML, Scheme, SmallTalk, or C++, and before learning Aldor I had never really used AXIOM. So my background is really ``orthogonal'' to the roots of Aldor. Nonetheless, I found Aldor easy to ``get into''. Some comments refer to the environment in which Aldor is used, not Aldor per se. However, as a typical user will come across these as well, they remain part of these Aldor experiences.

[Editor's note. Readers may find problems described here which are no longer encountered in the current version of Aldor. However, the problem-solving approach should still be found useful and, since the status of a ``novice'' cannot be re-created, no attempt has been made to recast the author's descriptions to match the behaviour of the current system.]

22.2 : First vignette: a modified factorial function

The first thing I did when I wanted to learn how to write an Aldor program was to type in and modify a model program. I chose the factorial program (from section23.2) first.

The final version of my modified file, complete with comments, is in figure 22.1.
Figure 22.1: Modified factorial program 

#include "aldor.as"

fact(n:Integer):Integer == {
        if n < 0 then error "Boom!"
        else if n < 2 then 1
        else n*fact(n-1) ;
}

import from Integer;

print << fact 7    << newline;
print << fact 78   << newline;
print << fact(-3)  << newline;
-- The following call never occurs, because the error above stops
-- the file from being read further.
print << fact 0    << newline;


22.2.1 : Lessons learned in writing this program

1.
Comments are marked with - at their beginning.
2.
You have to put quotes around the argument to #include.
3.
Parentheses  are necessary to prevent ambiguity in fact(-3). Note that parentheses are not always necessary for function application, in the absence of ambiguity: fact 7 is the same as fact(7).
4.
error prints a message and then stops the program.
5.
To put a newline after the output, put << newline after the print command.
6.
To get results printed, say print.
7.
You need import from Integer to use integers -- not inside procedures with formal parameters of type Integer, though, as the compiler is smart enough to figure out that you will need the operations from types you declare.
8.
Terminate statements with a ";".
9.
The ``suspicious juxtaposition'' error message means you forgot a semicolon.
Figure 22.2: Leaving out "import from Integer" 
    "fact.as", line 25: print << fact 7    << newline;
                    ..............^
[L25 C15] #1 (Error) No meaning for integer-style literal `7'.

"fact.as", line 26: print << fact 78   << newline;
                    ..............^
[L26 C15] #2 (Error) No meaning for integer-style literal `78'.

"fact.as", line 27: print << fact(-3)  << newline;
                    ..............^^
[L27 C15] #3 (Error) There are no suitable meanings for the 
operator `-'.
[L27 C16] #4 (Error) No meaning for integer-style literal `3'.

"fact.as", line 30: print << fact 0    << newline;
                    ..............^
[L30 C15] #5 (Error) No meaning for identifier `0'.

This is a ``sanitized'' version of my first program, in the sense that it works now. Of course, the program went through several iterations. The output of the program is now

(except that I manually split the big integer answer for factorial 78 over two lines). The answers are correct, as can be verified by comparing them with Stirling's formula and counting the zeros (there are fifteen 5's in 78 and three 25's, making eighteen factors of 5 in factorial 78, which gives eighteen trailing zeros).

It would, perhaps, be more useful to have presented seven variations of this program, removing an error each time (which is more or less how it was created) but I think that just reading the ``lessons learned'' in the comments above gives the flavour. It is useful to see two of the error messages from the compiler, though. Suppose we comment out the line import from Integer. Then the error messages we get are shown in figure 22.2;. tmoderr1Leaving out import from Integerexamples/moderr1.out I found them very puzzling to begin with. The compiler does not use its knowledge about Integers unless you tell it that it can -- but this is a feature: after all, we might have wanted to use the single precision kind, SingleInteger, instead of the infinite precision kind.

Figure 22.3: Leaving off a semicolon 

    "fact.as", line 25: print << fact 7    << newline
                    ......................^
[L25 C23] #2 (Error) There are no suitable meanings for 
		     the operator `newline'.

"fact.as", line 26: print << fact 78   << newline;
                    ^
[L26 C1] #1 (Warning) Suspicious juxtaposition.  Check for missing `;'.
Check indentation if you are using `#pile'.

Let's put the import from Integer statement back in and investigate another error message. Suppose that we leave the semicolon off the first print statement. Then compilation produces the error messages in figure 22.3;

In fact, the error messages have improved since I first wrote that program: now, it is clear that a missing semicolon is causing the problem. What about the first error though? What does There are no suitable meanings for the operator `newline' mean? The compiler interpreted lines 25 and 26 as a one-line statement, juxtaposing newline and print. If there had been an operator named newline which took as arguments something of the same type as print, then the compiler would have thought we meant newline(print) -- that is, apply the operator newline to the object print. That is what the compiler is complaining about -- it couldn't find any suitable operators called newline (and a good thing, too, because that isn't what I meant).

22.3 : Second vignette: the Lambert W function

22.3.1 Mathematics of W

22.3.2 The program

22.3.3 Lessons learned in writing this program

Let's now look at a simple program to evaluate a mathematical function known as the Lambert W function;(see the paper ``The Lambert W Function'', by Corless, Gonnet, Hare, Jeffrey and Knuth, or the article ``The Lambert W Function in Maple'', in the Maple Technical Newsletter no. 9). The mathematics for this programming example is encapsulated below. You may skip directly to section  if you wish: you need only know that this procedure computes the values of a mathematical function.

22.3.1 : Mathematics of W

The program uses a third-order accurate variant of Newton's method known as Halley's method to solve the equation defining the Lambert W function, namely

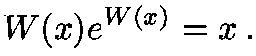
Originally, the program just used the initial guess w0 = 0, but this is a very poor starng pointt and we can do better. The program now uses three different initial guesses, depending on the value of x. If -1/e <= x < -.26, we use the initial guess

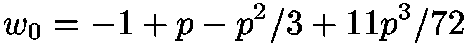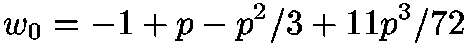
where p2 = 2(ex + 1). This uses the first four terms of the series expansion of W(x) about the branch point x=-1/e. It is exact if x = -1/e, and out by about 0.2 at the origin.

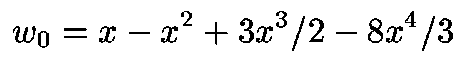
which uses the first four terms of the Taylor series expansion for W(x) about x=0. The magic number -0.26 was chosen because the two initial guesses agree near there.

The third initial guess is from an asymptotic series. If x >= 2 we use

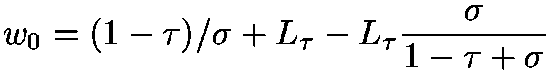
where 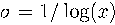, , 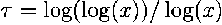and .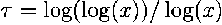

22.3.2 : The program

The program appears below. The line numbers  are added for this book -- they have no meaning for Aldor (and indeed if you type them in you will get a syntax error).



22.3.3 : Lessons learned in writing this program

1.
You do not need to declare the type of every variable. Some types can be figured out by the compiler automatically.
2.
Import everything you need.
3.
Put .0 after floats to distinguish them from integers.
4.
Semicolons separate statements in functions.
5.
(Second round) I like the ``suspicious juxtaposition'' warning. I had forgotten a semicolon.  
6.
You don't need a semicolon after } (or before it, either).
7.
A nifty way of doing cases is with =>. Count your ()'s carefully, though, because (a; b; c) is legal Aldor.
8.
You can declare more than one local (of the same type) in one statement.

The output is as below:

We can see that Aldor breaks floating-point numbers up into groups of ten when it prints, and that it doesn't print trailing zeros. We also see that we get to choose how many digits to use for floating-point arithmetic.

Remarks and Questions. It occurs to me now, as I write this, that I may sometimes want to evaluate this function over SingleFloat or DoubleFloat (for efficiency reasons, because that arithmetic can be performed in hardware), or in interval arithmetic (for guaranteed accuracy), or over complex forms of any of those. So I should think about writing a ``generic'' version of this program which is ``parameterized'' by the domain I wish to work in.

If this were AXIOM and I were a pure mathematician, I might try to make this program work for an arbitrary field -- but that is too general an object, because I also need the function ex as well as the field operations. And, thinking a bit more, we see that strictly speaking a field is too restrictive anyway: for Floats, associativity of + does not hold (try adding a very large number plus its negative plus 1 with different groupings; in one case you will get zero and in the other you will get 1). So we will need to define a new class of object, an ``arithmetic system'' if you will, that includes any object which has the field operations (but may not satisfy the field axioms). A useful subclass of this would consist of sets which allowed elementary functions, such as ex, sin x, to be defined on them. Clearly, this is something to be mulled over a bit more. On with the Aldor vignettes.

As a parting shot, I note that the program for the Lambert W function can be compiled successfully against the AXIOM library and used from within AXIOM, with only a trivial change. Since AXIOM used ** instead of ^ for raising to a power, line 31 of the program had to be changed. In addition, AXIOM refused to compute 1 - digits() because the answer might be a negative integer, whereas digits() must return a positive integer. To avoid this over-niceness, we rewrite line 31 with 10.0/10.0**digits() instead. After that change, the program works inside of AXIOM. Some other programs from this chapter are not yet able to be compiled against the AXIOM library.

22.4 : Third vignette: binary doubling

22.4.1 Binary doubling: theory

22.4.2 The program and results

22.4.3 Lessons learned in writing this program

This next example looks at binary doubling as a method of embedding integers into any arithmetic system. The original motivation for this program was that in an earlier version of the program compact.as (which is covered in the next vignette) I needed to be able to embed integers into an arbitrary field. The program turned into a nice Aldor exercise all on its own, and I probably learned more from it than I did from the compact finite difference program that motivated it.

While I was writing this program, the developers went ahead and included the functionality in the library, so this program is not, in fact, necessary. Further, there is a package for binary powering (see section 26.2;) which implements these same ideas still more efficiently. Nonetheless, this program taught me a lot and hence is included here.

22.4.1 : Binary doubling: theory

Skip this paragraph if you know how binary doubling or binary powering works, and go straight to section 22.4.2. Binary doubling is a reasonably efficient way of computing n x when all you can do is add things like x together. We are going to use it to compute n x 1 where 1 is the unit of the field under consideration. The basic idea is that we put q = c + vs where c =0, s = 1, and v = n initially, and test the bits of n. (Binary powering uses q = c sv, with appropriate changes in the initial values.) If the lowest-order bit of n is 1, then v is odd, and we rearrange q = c + vs as (c + s) + (v - 1)s. Thus, we can replace c by c+s and v by v-1. If instead the lowest-order bit of n is zero, then v is even, and we can rearrange q = c + vs as c + (v/2)(s + s). Thus we can replace s by s+s and v by v/2. Of course, we needn't actually carry out the division of v by 2 because that's just shifting, and we can implicitly do that just by looking at the next order bit of n. Note that our answer is always equal to q, and that each operation decreases the integer v. When v = 0, we know q = c, and we are finished.

22.4.2 : The program and results

The code, which is found below, contains an example of a ``generic'' function. The function accepts as input three things: an integer of one type or another (e.g. Integer or SingleInteger), its type, and the type of the output that is desired, which must be one ArithmeticSystem or another (for example, SingleFloat is an ArithmeticSystem because it has +, -, and *, though these operations need not (and do not) satisfy the axioms defining a ring, which imply, for example, that a + (b + c) = ((a + b) + c).

The fact that we can ``parameterize'' algorithms by the type of input and output is very powerful, and a major reason to learn Aldor. It allows us to write code once for a very wide variety of applications.

The output from this program was:

and this is correct. Note that trailing zeros are trimmed from floating point output.

22.4.3 : Lessons learned in writing this program

1.
Putting the parameters in the order 
    foo(n:I, I:IntegerNumberSystem, ...)

doesn't work, because, when the signature is being compiled, n:I can't be figured out. Instead, you have to put I:IntegerNumberSystem first. Perhaps this could be changed in a later release.

2.
It isn't necessary for locals to be declared explicitly, and in fact the program can be shorter and more readable if they aren't. However, if you don't declare a local explicitly, say in a procedure which is contained in a file, say file1, and if this file is #included into another file, say file2 which declares a global variable with the same name, then the compiler, when it sees file2, will produce a warning message telling you about the duplication. Explicit declaration of locals will prevent this warning message from being issued. Addendum to the lesson: Using #include is possible, but rarely done if the included files were written by someone else. Separate compilation is by far to be preferred, and if file1 and file2 are compiled separately, then it is safe to use implicit declarations.
3.
length(Integer):SingleInteger exists. I don't know what happens if the Integer is so long that its length doesn't fit in a SingleInteger (and I hope never to find out). The number would be slightly more than a billion digits long, and would require about 1.5 billion field + operations to embed in the field. Addendum: An ``engineering decision'' was made here: if you have an integer so long that its length doesn't fit into a SingleInteger, then that integer will take up an eighth of your address space; it was decided that length will just return the wrong answer in that case.
4.
230 is used as a SingleInteger example, since 231 is too big to fit in a SingleInteger and so looks like a negative number. ``That's not a bug, that's a feature''. Caveat emptor.
5.
import from Integer at the bottom of the file is no different from import from Integer at the top of the file. So, even though I did that import below the calculation of 230, the types involved can't be figured out automatically. (Is it SingleInteger to the SingleInteger or are Integers involved?) import

6.
This whole procedure might have been necessary at one time, but the development team is too fast for me. It's already there! The construct 3::F could now be used to coerce 3 into being an element of an ArithmeticSystem, F. So this program was a fun exercise but, ultimately, a reinvention.

7.
Maybe this program is efficient, but it isn't optimal. The operations can be done ``in place'' and if our field consists of million-by-million matrices, that could make a major difference. See the BinaryPowering package in section 26.2.

8.
The result of length(0) is 0 and of length(1) is 1. The program bit(m,n) returns the n bit of m, not the other way around. You can find this out from the manual, but it is easier to write an Aldor program which prints out the length of various numbers and the various bits of a number, say 23.


22.5 : Fourth vignette: compact finite differences

22.5.1 Mathematics of compact finite differences

22.5.2 Lessons learned in writing this program

22.5.3 Testing

22.5.4 Lessons learned in writing this program

Now we look at some code which uses ``compact finite differences'' to find fourth-order accurate approximations to the derivative of a function given on a grid of equally-spaced values. The technique of compact finite differences is more general than this, but for this application has an interesting advantage: we can choose the formulas so that the tridiagonal matrix that occurs in the evaluation of the finite differences can be factored exactly. This leads to a very efficient algorithm.

The program is as below. My original version of this program used the ``embed'' program discussed in the previous vignette. However, that was superseded by the library coercion of integers into arbitrary fields: as a result, the code is now much shorter and easier to read. There remains a section which explicitly tells the compiler how to multiply elements of the field by integers, and similarly for other operations. Perhaps that, too, will soon be unnecessary.

22.5.1 : Mathematics of compact finite differences

Skip this section if you like.

Compact finite differences are a relatively new method of efficiently approximating derivatives. The basic trick is that instead of the usual explicit formulas for finite differences, for example:

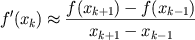
which we use at every interior grid point, we write down a (banded) linear system of equations for the unknown derivatives, for example: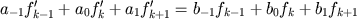



for k = 2, 3, ..., n - 1.

Together with equations for differences at the boundaries, this gives us a tridiagonal linear system to solve, to find the derivatives at all the grid points. This approach has several advantages:

1.
By keeping the difference scheme compact, we can achieve significant storage savings for a given order.
2.
By appropriate choice of the constants and the boundary formulas, we can choose the linear system to be particularly easy to factor and solve. We will do this below.
3.
We do not have to choose the parameters for accuracy: we can choose them to increase stability instead.

I implemented an Aldor program to find the fourth-order accurate approximation to the first derivatives on a uniform grid using the scheme

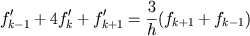
for k = 2, 3, ..., nn -1, and here I chose slightly different formulas for the endpoints so the linear system is

where the matrix A is
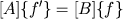
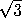The number c = 2 + was chosen so that A can be exactly factored into A = LU = LDLT where

a = 1/c and D = diag(c,c,...,c). (It turns out that c = 2 - 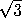would also work , here.) Then solving A {f '} = { b} can be reduced to the two trivial problems L{y} = {b} followed by U{x} = {y}. The solution of the system can therefore be expressed by the following recurrence relations:

y1 = b1
yk = bk - ayk-1

for k = 2,3,...,n, and
xn = ayn
xk = a(yk - xk+1)
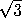for k = n-1,n-2,...,1. Note that the recurrence relations are linear and could be solved analytically, but for efficiency resons it is preferable not to do so. Also, if we had chosed c = 2 - above, then a = 2 + 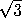and the solutions to the recurrence relation for yk would grow exponentially. This would certainly exacerbate the effects of rounding errors and so we avoid that possible pitfall by choosing c = 2 + 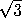instead. To see this another way, it can be shown that the condition number of L is K1(L) = (1 + a)(1 - an)/(1 - a), which, is we choose c = 2 + 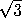(so that 0 < a = 1/c <1) can be shown to give K1(A) = K1 (LDL T) = K12(L) ~ (2 + 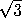) 2n which grows exponentially with n, which is clearly undesirable.)

22.5.2 : Lessons learned in writing this program

1.
Typing 103::F * x is no fun when you want 103*x to be automatic. With the current compiler, it's cleaner to add eight one-line programs which define integer*field etc. These are the lines marked by -*-*-*-* in the program on. (These may be subsumed by library code at some future release).
2.
# funvals gives you the size of the Array. ``PrimitiveArrays'' don't know how big they are but ``Arrays'' do.
3.
new(n,0) creates a new array (list or whatever) of size n with each element initialized to zero.
4.
To see why the construct 1@F is occasionally necessary in statements like (3*c-1@F), let us look at what happens while it is being evaluated...

The compiler automatically figures out that 3*c is an element of an ArithmeticSystem and evaluates this by a call to the particular multiplication routine which takes ``SingleIntegers'' as its first argument and ArithmeticSystem elements as its second argument, however...

It turns out that there are two possible routines that could be used to subtract 1 from an ArithmeticSystem element: namely, one that takes an integer as its second argument and one that takes an ArithmeticSystem element there - this is because 1 is already an ArithmeticSystem element (both 1 and 0 are members of any ArithmeticSystem).

Now, the routine that takes (x:F) - (y:F) to F will give the same results as the one that takes (x:F) - (n:SI) to F, because the second actually does a coercion and calls the first -- but the Aldor compiler isn't (yet) smart enough to figure out that hierarchy. So we have to help Aldor out by telling it which routine to use, and the simplest solution is to force the choice by using 1@F.



22.5.3 : Testing

We need to test this program. The program below gives a simple test, to ensure that no blunders were committed.

The results are

We can see that the errors are O(h4) as promised.

22.5.4 : Lessons learned in writing this program

1.
If you don't import from Integer, then the squaring operator ^2 is not defined. You can rewrite x^2 as x*x to avoid importing from Integer. This saves confusion if ``SingleIntegers are present.
2.
Arrays and vectors can be referenced with parentheses (( )).
3.
You can #include other .as files just like you can the library. You can nest #include#includes as well.
4.
We needed a square root function, which is present in Aldor for DoubleFloat, but needs some extra work (at present) to make it accessible: namely, we had to extend DoubleFloat to have a square root function in it.
5.
Use readline! and scanNumber to read in numeric data.
6.
To compile against a library is superior to nesting #include statements.
7.
Turning the optimization on makes the code go really fast. Times are (roughly) 3 seconds to solve a system with 30000 grid points, on an IBM RS6000 model 530.
8.
You can import from several packages at once.


22.6 : Fifth vignette: rounded rationals

This last vignette demonstrates the most powerful features of Aldor I have used to date. Paradoxically, however, it was one of the easiest programs to write. It appears to be generally true that writing ``parameterized types'' is even easier than writing ordinary functions.

What are ``rounded rationals''? They are ordinary rational numbers, restricted so that their denominators do not grow ``too big''. They are like floating- point numbers in many ways: for example, they are not exact, and they can be implemented efficiently. Suppose we are working with rationals rounded so that the denominators cannot exceed 9 (that is, only one-digit denominators are allowed). Then if we add 1/2 + 1/3, we can get 5/6 exactly right in this system, but if we add 1/4 + 1/7 we get 11/28, which cannot be represented in this system, and we round to the nearest, namely 2/5. How do we know 2/5 is the closest one-digit denominator rational to 11/28? The answer lies in the classical theory of simple continued fractions.

We expect that all the usual rational arithmetic operations will be available for rounded rationals, with the understanding that results of the operations +, -, *, and / will be rounded to nearest.

22.6.1 : Simple continued fractions: theory

22.6.1 Simple continued fractions: theory

22.6.2 Lessons learned in writing the program

22.6.3 Testing

22.6.4 Lessons learned in writing the program

This section can be skipped, once you realize that it defines a ``magic algorithm'' that finds the nearest rational number with denominator within the limits. A simple continued fraction (see C. D. Olds, Continued Fractions, Dover) is a fraction of the form

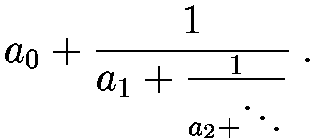
The next paragraph explains how we can compute a continued fraction for a rational number by (essentially) the Euclidean algorithm for finding the greatest common divisor of two integers.

Recall that the Euclidean algorithm runs as follows: given two integers a and b as input, we put e0 = a > e1 = b (interchanging a and b if necessary so that a > b), and the numbers ak and ek in the followig sequence:

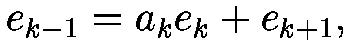
that is to say, defining ek+1 as the (integer) remainder on dividing ek-1 by ek, and defining the integers ak as the quotients that arise. We terminate the computation when some ek = 0, which must eventually happen since 0 <= ek+1 by the properties of the division algorithm.

Now suppose that we wish to compute a continued fraction expansion for a/b. Then

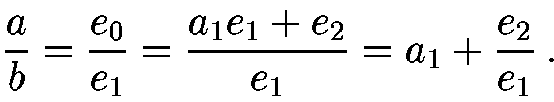
The main trick is now to rewrite e2/e1 as the reciprocal of its reciprocal:

and at last

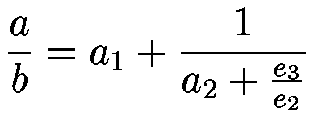
This process is continued in the obvious way, which is to replace e3/e2 recursively by its continued fraction.

Therefore, given a rational number x we can find its continued fraction by the Euclidean algorithm, so the cost of finding the continued fraction is no more than the cost of computing a GCD (in the naive way). What happens if instead we are given the continued fraction first? It turns out that, given the partial quotients ak of the continued fraction, we can compute a sequence of approximants xk = pk/qk by the following recurrences, with p0 = a0, q0 = 1, p-1 = 1 and q-1 = 0.

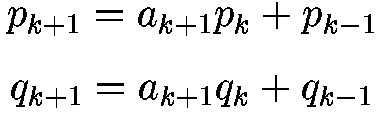
These approximants have a ``best approximation'' property: pk/qk is the best approximation to x with denominator smaller than qk2.

The algorithm we will use should be obvious now. Given two rounded rationals and an operation to perform on them, we first perform the operation exactly and then round the result to the nearest acceptable rational by computing the partial quotients of our result, until the denominator of xk exceeds the maximum allowed. The code below does exactly that. I did not write this code from scratch: I looked at the source code for Ratio, which I found in the file

$ALDORROOT/samples/libaldor/ratio.as
and modified that (no, that's not cheating).

22.6.2 : Lessons learned in writing the program

1.
By convention, capitalizations indicate types. Therefore Rep is a type, as is RoundedRatio -- but rep, on the other hand, is a way to cast something into its representation.
2.
Records are easy.
3.
Exports: some are automatic, for example if you are building an OrderedRing or Field. In that case, things like %^Integer have to be made. (Though you may make them give an error message, as Ratio used to do.)
4.
You break out of a loop with break.
5.
ArithmeticSystems require +, - , * but not divide (/) -- however, adding this is okay. We also want to add I + % etc. ArithmeticSystems also require integer powering.
6.
Field is also necessary for some applications. It is not subsumed by ArithmeticSystem (or vice versa) because each provides some operations the other lacks. To find out what a type really needs to provide, you can use the documentation or the ``interactive mode'': 
    % aldor -gloop
%1 >> #include "aldor"
%2 >> ArithmeticSystem
  () @ Third( with
        0: %
        +: % -> %
        +: (%, %) -> %
        -: % -> %
        -: (%, %) -> %
        1: %
        *: (%, %) -> %
        ^: (%, Integer) -> %
        coerce: Integer -> %
        coerce: SingleInteger -> %) ==  with
        0: %
        +: % -> %
        +: (%, %) -> %
        -: % -> %
        -: (%, %) -> %
        1: %
        *: (%, %) -> %
        ^: (%, Integer) -> %
        coerce: Integer -> %
        coerce: SingleInteger -> %

So we must, necessarily, provide ten operations (those listed after the first ``with''). This ArithmeticSystem will provide more functionality, so we will have to add more operations.



22.6.3 : Testing

This implementation of a type needs to be tested. Evaluating a polynomial at 1000 points on an interval and comparing the results with the exact results might be one way to do it. Another is to do the compact finite difference problem with ``Rounded Rationals'' instead of DoubleFloats, and see if the errors are of similar size.

Typical output is shown below.

The similarity of behaviour is a good indicator that things are (now) working correctly. I had to add a routine root3 which calculated the square root of 3 as a rounded rational. I could have written a general square root program, but it seemed easiest to use the known simple continued fraction, 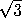= 1 + [1,2,1,2,1,2,...], to do the job here.

22.6.4 : Lessons learned in writing the program

1.
This turned out to be a very useful test for the Rounded Rational type. I learned (again) that SingleIntegers which are too large become negative (that's not a bug, I'm told, it's a feature). This leads to incorrect results if your intermediate results are large. Since I don't want incorrect results, however quickly they are obtained, I would like to see some feature in Aldor to allow me to generate an error message if a SingleInteger overflows. It has been suggested that what I wanted was CheckedSingleInteger (which will presumably be implemented in a later release), and I concur.

I have fixed the program so that choosing MAXINTSIZE smaller than 32768 will avoid any of these overflows with SingleInteger. This provides roughly the same precision as ``single precision'' floating point arithmetic, namely that numbers can be represented accurately to 1 part in 230.

In searching for the cause of that problem, I was forced to go over the code for RoundedRatio very carefully, and I found several potential bugs: in particular I found some places where I was not careful to keep the denominators positive. (I also discovered that you can't name your program file what, apparently because it interferes with a Unix command of the same name.)

2.
I also learned more thoroughly how to compile against a library. You need to say .ao in the #library command, and to include the .ao file in the compile command.
3.
Compiling with option -M no-mactext means that errors involving macros are pointed to where they occur, and not where the macro is defined. This made several error messages much clearer.
4.
1@R means ``I know this 1 is ambiguous, but pick the 1 from R''. It's different from 1::R, which might mean coerce the SingleInteger 1 to type R or coerce the Integer 1 to type R.
5.
You can input numbers from the keyboard by reading a string using the CommandLine, Array(String), InFile and StandardIO types, together with the NumberScanPackage.
6.
Coercion to DoubleFloats is easy. It ought to be only slightly harder to write a coercion the other way. (Continued fraction algorithms are helpful here too.)
7.
Printing of rational numbers sometimes requires a demarcation to separate side-by-side rationals easily (otherwise you might get things like 1/24/3 instead of (1/2)(4/3) -- obviously spaces might help too). Ratio Integers are printed with parentheses (( )). I chose to print Rounded Rationals with angle brackets (< >).


22.7 : Retrospective

Though I have really only been programming in Aldor for about three weeks (not counting time spent doing other things), I don't consider myself an Aldor novice anymore. Of course, I still have an enormous amount to learn (I now know that I haven't even peeled off more than one or two layers of the ``onion'') but I can now make Aldor do nontrivial tasks, efficiently and easily. I want to use Aldor to investigate Gröbner basis algorithms for polynomials with rounded rational coefficients, to solve delay differential equations and to implement an efficient and useful interval arithmetic. I have some confidence that all these will be possible -- and interesting.

I also have the feeling that Aldor is an efficient, powerful and elegant language. It is still in its infancy, so I am really talking about ``potential'' here. But if this is an infant, what will the adult be like?

Previous Home Contents Next