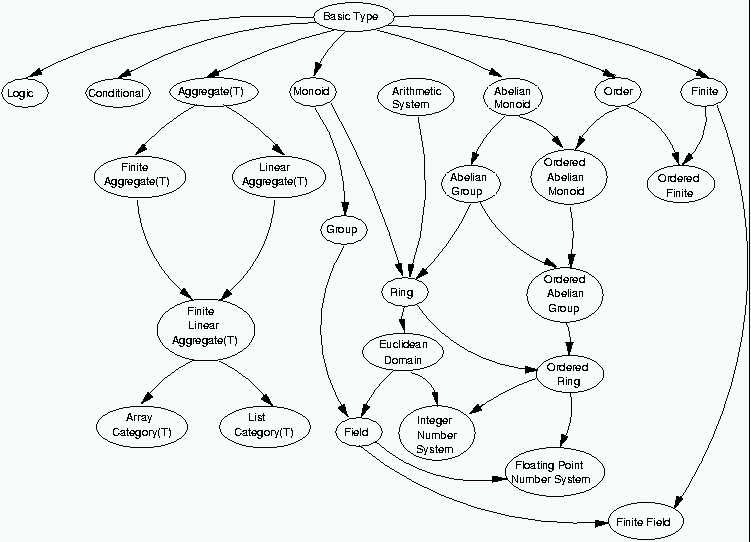
Chapter 25: The base library categories

Directly inherits:
BasicType

Exports:

empty?: % -> Boolean Is the element count zero?
generator: % 0> Generator(S) Generic traversal of an aggregate.
map: (S -> S, %) -> % Form new aggregate using function.
=: (%, %) -> Boolean	from BasicType
~=: (%,%) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType

Definition:

define Aggregate(S: Type): Category == BasicType with {
        empty?:   % -> Boolean;
        generator:% -> Generator S;
        map:      (S->S, %) -> %;

        export from S;
}

25.4 : ArithmeticSystem

Directly inherits:
(none)

Exports::

0: % Indentiyt for `+'.
+: % -> % Identity function.
+: (%, %) -> % Addition.
-: % -> % Negation.
-: (%, %) -> % Substraction.
1: % Identity for `*'
*: (%, %) -> % Multiplication
^: (%, Integer) -> %
coerce: Integer -> %;
coerce: SingleInteger -> %

Definition:

define ArithmeticSystem: Category == with {
        0:      %;
        +:      % -> %;
        +:      (%, %) -> %;
        -:      % -> %;
        -:      (%, %) -> %;

        1:      %;
        *:      (%, %) -> %;
        ^:      (%, Integer) -> %;
}

25.5 : ArrayCategory S

Parameter:

Directly inherits:
FiniteLinearAggregate(S)

Exports:

set!: (%, SingleInteger, S) -> S `set!(a,n,s)' sets the nth element of `a' to `s'.
dispose!: % -> () `dispose!(a)' indicates that `a' will no longer be used.

Definition:

define ArrayCategory(S: Type): Category == FiniteLinearAggregate S with {
        set!: (%, SingleInteger, S) -> S;
        dispose!: % -> ();
}

25.6 : BasicType

Directly inherits:
(none)

Exports:

=: (%, %) -> Boolean
~=: (%, %) -> Boolean Equality and inequality test.	[default]
<<: (TextWriter, %) -> TextWriter
<<: % 0> TextWriter -> TextWriter Basic output.	[default]
sample: % Example element.
hash: % -> SingleInteger Hashing function.	[default]

Definition:

define BasicType: Category == with {
        =:      (%, %) -> Boolean;
        ~=:     (%, %) -> Boolean;
        <<:     (TextWriter, %) -> TextWriter;
        <<:     % -> TextWriter -> TextWriter;
        sample: %;
        hash:   % -> SingleInteger;

        default (x: %) ~= (y: %): Boolean == not (x = y);
        default hash(x: %): SingleInteger == (0$Machine)::SingleInteger;
        default (<<)(x: %)(p: TextWriter): TextWriter == p << x; 
}

25.7 : Conditional

Description:
`Conditional' allows values to be used in conditional context, such as in an `if' or in a `while'.

Directly inherits:
BasitType

Exports:

test: % -> Boolean Test used in conditional context.
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType

Definition:

define Conditional: Category == BasicType with {
        test:     % -> Boolean;
}

25.8 : ElementaryFunctions

Description:
`ElementaryFunctions' provides the basic trigonometric and exponential function and their inverses.

Directly inherits:
(none)

Exports:

^: (%, %) -> % General exponentiation.
exp: % -> % Exponential of `e'.
log: % -> % Natural logarithm.
log10: % -> % Logarithm base 10.
sin, cos, tan: % -> % Circular trigonometric sine, cosine, tangent.
sinh, cosh, tanh: % -> % Hyperbolic trigonometric sine, cosine, tangent.
asin, acos, atan: % -> % Functional inverse of `sin', `cos', `tan'.
asinh, acosh, atanh: % -> % functional inverse of `sinh', `cosh', `tanh'.
sqrt: % -> % Square root.
root: (%, SingleInteger) -> % General surd.

Definition:

define ElementaryFunction: Category == with {
        exp:    % -> %;

        sin:    % -> %;
        cos:    % -> %;
        tan:    % -> %;

        sinh:   % -> %;
        cosh:   % -> %;
        tanh:   % -> %;

        log:    % -> %;
        log10:  % -> %;

        asin:   % -> %;
        acos:   % -> %;
        atan:   % -> %;

        asinh:  % -> %;
        acosh:  % -> %;
        atanh:  % -> %;

        sqrt:   % -> %;
        root:   (%, SingleInteger) -> %;
        ^:      (%, %) -> %;
}

25.9 : EuclideanDomain

Description:
`ElementaryFunctions' provides the basic trigonometric and exponential

Directly inherits:
Ring

Exports:

0: %	from ArithmeticSystem
1: %	from ArithmeticSystem
+: % -> %	[default]from ArithmeticSystem
+: (%, %) -> %	from ArithmeticSystem
-: % -> %	from ArithmeticSystem
-: (%, %) -> %	[default] from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem
coerce: SingleInteger -> %	from ArithmeticSystem
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
zero?: % -> Boolean	[default] from AbelianMonoid
gcd: (%, %) -> % Greatest common divisor.
quo: (%, %) -> % Quotient leaving remainder.
rem: (%, %) -> % Remainder.
divide: (%, %) -> (%, %) Quotient-remainder pair.	[default]
sample: %	[default] from BasicType
hash: % -> SingleInteger	[default] from BasicType

Definition:

define EuclideanDomain: Category == Ring with {
        gcd:    (%, %) -> %;
        quo:    (%, %) -> %;
        rem:    (%, %) -> %;
        divide: (%, %) -> (%, %);

        default divide(a: %, b: %): (%, %) == (a quo b, a rem b);
{

25.10 : Field

Description:
`Field' prvides arithmetic with division.

Directly inherits:
EuclideanDomain, Group

Exports:

/: (%, %) -> % Division: a / b = a * inv(b).	[default]
\: (%, %) -> % Division: a \ b = inv(a) * b.	[default]
inv: % -> % Inverse.
0: %	from ArithmeticSystem
1: %	from ArithmeticSystem
+: % -> %	[default]from ArithmeticSystem
+: (%, %) -> %	from ArithmeticSystem
-: % -> %	from ArithmeticSystem
-: (%, %) -> %	[default] from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem
coerce: SingleInteger -> %	from ArithmeticSystem
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
zero?: % -> Boolean	[default] from AbelianMonoid
gcd: (%, %) -> %	[default] from EuclideanDomain
quo: (%, %) -> %	[default] from EuclideanDomain
rem: (%, %) -> %	[default] from EuclideanDomain
divide: (%, %) -> (%, %)	[default] from EuclideanDomain
sample: %	[default] from BasicType
hash: % -> SingleInteger	[default] from BasicType

Definition:

define Field: Category == Join(EuclideanDomain, Group) with {
        default {
                gcd(a: %, b: %): % == {zero? a and zero? b => 0; 1}
                (a: %) quo (b: %): % == a/b;
                (a: %) rem (b: %): % == 0;
        }
}

25.11 : Finite

Description:
`Finite' indicates that a type has only a finite number of values

Directly inherits:
BasicType

Exports:

#: Integer Number of values in the type.
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType

Definitoin:

define Finite: Category == BasicType with {
        #: Integer;
}

25.12 : FiniteAggregateS

Description:
`FiniteAggregate(S)' provides operations for manipulating structures representing finite collections of values of type `S'.

Parameter:

Directly inherits:
Aggregate(S)

Exports:

#: % -> SingleInteger Count of the number of elements.
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) => TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
empty?: % -> Boolean	[default] from Aggregate(S)
generator: % -> Generator(S)	from Aggregate(S)
map: (S -> S, %) -> %	from Aggregate(S)

Definition:

define FiniteAggregate(S: Type): Category == Aggregate S with {
        #:        # -> SingleInteger;

        default empty? (a: %) : Boolean == {
                import from SingleInteger, Machine;
                ((#a)::SInt = 0)::Boolean;
        }
}

25.13 : FiniteField

Description:
`FiniteField provides arithmetic on a finite set.

Directly inherits:
Finite, Field

Exports:

integer: Literal -> %
reduce: SingleInteger -> %
lift: % -> SingleInteger
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	[default] from BasicType
hash: % -> SingleInteger	[default] from BasicType
#: Integer	from Finite
0: %	from ArithmeticSystem
+: % -> %	[default] from ArithmeticSystem
+: (%, %) -> %	from ArithmeticSystem
-: % -> %	from ArithmeticSystem
-: (%, %) -> %	[default] from ArithmeticSystem
1: %	from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem
coerce: SingleInteger -> %	from ArithmeticSystem
zero?: % -> Boolean	[default] from AbelianMonoid
gcd: (%, %) -> %	[default] from EuclideanDomain
quo: (%, %) -> %	[default] from EuclideanDomain
rem: (%, %) -> %	[default] from EuclideanDomain
divide: (%, %) -> %	[default] from EuclideanDomain
/: (%, %) -> %	[default] from Group
\: (%, %) -> %	[default] from Group
inv: % -> %	from Group

Definition:

define FiniteField: Category == Join(Finite, Field) with {
        integer:Literal -> %; 
        reduce: SingleInteger -> %;
        lift:   % -> SingleInteger;
}

25.14 : FiniteLinearAggregate S

Description:
`FiniteLinearAggregate(S)' provides operations for manipulating structures representing finite linear collections of values of type `S'.

Parameter:

Direclty inherits:
FiniteAggregate(S), Linear Aggregate(S)

Exports:

=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) => TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
empty?: % -> Boolean	[default] from Aggregate(S)
generator: % -> Generator(S)	from Aggregate(S)
map: (S -> S, %) -> %	from Aggregate(S)
#: % -> SingleInteger	from FiniteAggregate(S)
empty: () -> %	[default] from LinearAggregate(S)
bracket: Generator(S) -> %	LinearAggregate(S)
bracket: Tuple(S) -> %	LinearAggregate(S)
map: ((S, S) -> S, %, %) -> %	[default] LinearAggregate(S)
apply: (%, SingleInteger) -> S	LinearAggregate(S)

Definition:

define FiniteLinearAggregate(S: Type): Category ==
        Join(FiniteAggregate S, LinearAggregate S);

25.15 : FloatingPointNumberSystem

Description:
`FloatingPointNumberSystem' provides the basic operations for a type which approximates the real n8umbers as a floating point system.

Directly inherits:
OrderedRing, Field

Exports:

float: Literal -> % Floating point-style literals.
<<: (%, %) -> Boolean Insignificance: a << b => a + b = b
>>: (%, %) -> Boolean Dominance: a >> b => a + b = a
step: SingleInteger -> (%, %) -> Generator(%) `step(n)(a,b)' yields `n' evenly separated values on `a, b'
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) => TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
<, >, <=, >=: (%, %) -> Boolean	from Order
<, >, <=, >=: (%, %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Boolean	[default] from Order
min, max: (%, %) -> %	[default] from Order
0: %	from AbelianMonoid
+: % -> %	[default from AbelianMonoid
+: (%, %) -> %	from AbelianMonoid
zero?: % -> Boolean	[default] from AbelianMonoid
-: % -> %	from AbelianGroup
-: (%, %) -> %	[default] from AbelianGroup
1: %	from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem
coerce: SingleInteger -> %	from ArithmeticSystem
abs: % -> %	[default] from OrderedRing
sign: % -> %	[default] from OrderedRing
negative?: -> Boolean	[default] from OrderedRing
positive?: % -> Boolean	[default] from OrderedRing
gcd: (%, %) -> %	[default] from EuclideanDomain
quo: (%, %) -> %	[default] from EuclideanDomain
rem: (%, %) -> %	[default] from EuclideanDomain
divide: (%, %) -> (%, %)	[default] from EuclideanDomain
/: (%, %) -> %	[default] from Group
\: (%, %) -> %	[default] from Group
inv: % -> %	from Group

Definition:

define FloatingPointNumberSystem: Category ==
                 Join(OrderedRing, Field) with {
        float:     Literal -> %;
        <<:        (%, %) -> Boolean;
        >>:        (%, %) -> Boolean;
        coerce:   Integer -> %; 
        coerce:   SingleInteger -> %;
        step:     SingleInteger -> (%, %) -> Generator %;
}

25.16 : Group

Description:
`Group' provides multiplicative arithmetic with division.

Directly inherits:
Monoid

Exports:

/: (%, %) -> % Division: a / b = a*inv(b).	[default]
\: (%, %) -> % Division: a \ b = inv(a)*b.	[default]
inv: % -> % Inverse.
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
1: %	from Monoid
*: (%, %) -> %	from monoid
^: (%, Integer) -> %	from Monoid

Definition:

define Group: Category == Monoid with {
        /:      (%, %) -> %;
        \:      (%, %) -> %;
        inv:    % -> %;
 
        default (a: %) / (b: %): % == a * inv b;
        default (a: %) \ (b: %): % == inv a * b;

25.17 : IntegerNumberSystem

Description:
`IntegerNumberSystem' provides the basic operations for a type which represents a range of integers.

Directly inherits:
OrderedRing, EuclideanDomain

Exports:

integer: Literal -> % Integer-style literals.
even?: % -> Boolean
odd?: % -> Boolean Tests whether the value is even or odd.
single?: % -> Boolean `single?(v) returns true if a SingleInteger can hold the value `v'.
prev: % -> %
next: % -> % Decrement/increment the value by 1.
mod: (%, %) -> % Modulus.
length: % -> SingleInteger -> % Length in bits.
shift: (%, SingleInteger) -> % Shift by the a number of bits.
bit: (%, SingleInteger) -> Boolean Extract the desired bit.
retract: % -> SingleInteger Covert to SingleInteger, if can.
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) => TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
<, >, <=, >=: (%, %) -> Boolean	from Order
<, >, <=, >=: (%, %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Boolean	[default] from Order
min, max: (%, %) -> %	[default] from Order
0: %	from AbelianMonoid
+: % -> %	[default from AbelianMonoid
+: (%, %) -> %	from AbelianMonoid
zero?: % -> Boolean	[default] from AbelianMonoid
-: % -> %	from AbelianGroup
-: (%, %) -> %	[default] from AbelianGroup
1: %	from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem
coerce: SingleInteger -> %	from ArithmeticSystem
abs: % -> %	[default] from OrderedRing
sign: % -> %	[default] from OrderedRing
negative?: -> Boolean	[default] from OrderedRing
positive?: % -> Boolean	[default] from OrderedRing
gcd: (%, %) -> %	[default] from EuclideanDomain
quo: (%, %) -> %	[default] from EuclideanDomain
rem: (%, %) -> %	[default] from EuclideanDomain
divide: (%, %) -> (%, %)	[default] from EuclideanDomain

Definition:

define IntegerNumberSystem: Category ==
             Join(OrderedRing,EuclideanDomain) with
{
        integer:   Literal -> %;
        even?:     % -> Boolean;
        odd?:      % -> Boolean:
        single?:   % -> Boolean:
        prev:      % -> %;
        next:      % -> %;
        mod:       (%, %) -> %;
        length:    % -> SingleInteger;
        shift:     (%, SingleInteger) -> %;
        bit:       (%, SingleINteger) -> Boolean;
        retract:   % -> SingleInteger;
}

25.18 : LinearAggregate S

Description:
`LinearAggregate(S)' provides operations for manipulating structures representing linear collections of values of type `S'.

Parameter:

Directly inherits:
Aggregate(S)

Exports: from BasicType

empty: () -> % Construction with no values.	[default]
bracket: Generator(S) -> % Construction from a generator.
bracket: Tuple(S) -> % Construction from a tuple.
map: ((S, S) -> S, %, %) -> % Element-wise combination.	[default]
apply: (%, SingleInteger) -> S
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %
hash: % -> SingleInteger	[default] from BasicType
empty?: % -> Boolean	from Aggregate(S)
generator: % -> Generator(S)	from Aggregate(S)
map: (S -> S, %) -> %	[default]from Aggregate(S)

Definition:

define LinearAggregate(S: Type): Category == Aggregate S with {
        empty:    () -> %;
        bracket:  Generator S -> %;
        bracket:  Tuple S -> %;

        map:      ((S,S)->S, %, %) -> %;
        apply:    (%, SingleINteger) -> S;

        default {
                empty(): % ==
                        [];
                map (f: S -> S, a:%): % ==
                        [f x for x in a];
                map (f: (S,S)->S, a: %, b: %): % ==
        }
}

25.19 : ListCategory S

Description:
`ListCategory' provides the basic operations for linked lists.

Parameter:

Directly inherits:
FiniteLinearAggregate(S), Conditional

Exports:

nil: % nil is a literal constant that is an empty list.
cons: (S, %) -> % `cons(s,k)' appends `s' to the front of the list `k'.
list: Tuple(S) -> %
list: Generator(S) -> % Generates a list from a tuple or a generator of `S'.
first: % -> S
rest: % -> % `first(k)' returns the first element of the list `k'. `rest(k)' returns the list consisting of all elements of k after the first.
setFirst!: (%, S) -> S
setRest!: (%, %) -> % `setFirst!(k, s)' destructively modifies the list `k' so that the first element is `s'. `setRest!(k1, k2) destructively modifies the list `k1' so that rest(k1) = k2.
apply: (%, 'first') -> S
apply: (%, 'rest') -> % `l.first' is equivalent to `first(l)'. `l.rest' is equivalent to `rest(l)'.
set!: (%, 'first', S) -> S
set!: (%, 'rest', %) -> % `l.first := v' is equivalent to `setFirst!(l,v)'. `l.rest := t' is equivalent to `setRest!(l, v, t)'.
copy: % -> % `copy(k)' returns a copy of the list `k'.
last: % -> S `last(k)' returns the last element of the list `k'.
reverse: % -> %
reverse!: % -> % `reverse(k)' non-destructively reverses the elements of `k'. `reverse!(k)' destructively reverses the elements of k.
concat: (%, %) -> %
concat!: (%, %) -> % `concat(k1,k2)' returns a new list that contains the elements of `k1' appended to the front of`k2'. `concat!(k1,k2)' destructively (to `k1') appends `k1' to the front of `k2'.
reduce: ((S, S) -> S, %, S) -> S `reduce(fun,k,s)' computes `r1 = fun(first k, s)', then `r2 = (fun first rest k, r1)' and so, returning the final value computed.
member?: (S, %) -> Boolean `member?(s,k)' returns true if `s' is contained in `k', false otherwise.
rest: (%, SingleInteger) -> % `rest(k,i)' drops the first `i' elements from `k'.
tails: % -> Generator(%) `tails(k)' returns the successive tails of `k'. Clients are allowed to call setFirst! and setRest! on the generated values.
dispose!: % -> ()
disposeHead!: % -> % `dispose!(1)' indicates the list `l' will no longer be used.
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
empty?: % -> Boolean	from Aggregate(S)
generator: % -> Generator(S)	from Aggregate(S)
map: (S -> S, %) -> %	[default]from Aggregate(S)
#: % -> SingleInteger	from FiniteAggregate(S)
empty: () -> %	[default] from LinearAggregate(S)
bracket: Generator(S) -> %	from LinearAggregate(S)
bracket: Tuple(S) -> %	from LinearAggregate(S)
map: ((S, S) -> S, %, %) -> %	[default] from LinearAggregate(S)
apply: (%, SingleInteger) -> S	from LinearAggregate(S)
test: % -> Boolean	from Conditional

Definition:

== Join(FiniteLinearAggregate S, Conditional) with {
   
        export from 'first';
        export from 'rest';

        nil: %;
        cons: (S, %) -> %;

        first: % -> S;
        rest: % -> %;

        setFirst!: (%, S) -> S;
        setRest!: (%, %) -> %;

        apply: (%, 'first') -> S;
        apply: (%, 'rest') -> %;

        copy: % -> %;
        last: % -> S;

        reverse: % -> %;
        reverse!: % -> %;
 
        concat!: (%, %) -> %;
        concat: (%, %) -> %;

        reduce: ((S, S) -> (S, %, S) -> S;
        member?: (S, %) -> Boolean;

        rest: (%, SingleINteger) -> %;
        tails: % -> Generator %;

        dispose!: % -> ();
        disposeHead!: % -> %;
}

25.20 : Logic

Description:
`Logic' provides the basic operations for lattices, e.g. Booleal algebra.

Directly inherits:
BasicType

Exports:

~: % -> % Logical complement
/\: (%, %) -> % Locical `meet', e.g. `and'
\/: (%, %) -> % Logical `join', e.g. `or'.	[default]
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType

Definition:

define Logic: Category == BasicType with {
       ~:         % -> %;
       /\:        (%, %) -> %;
       \/:        (%, %) -> %;
}

25.21 : Monoid

Description:
`Monoid' provides multiplicative arithmetic.

Directly inherits:
BasicType

Exports:

1: % Identity for multiplication.
*: (%, %) -> % Multiplication.
^: (%, Integer) -> % Exponentiation or error.
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> TextWriter	from BasicType

Definition:

define Monoid: Category == BasicType with {
        1:      %;
        *:      (%, %) -> %;
        ^:      (%, Integer) -> %;
}

25.22 : Order

Description:
`Order' provides operations for an order relation, `>', and its dual, `<'.

Direclty inherits:
BasicType

Exports:

>: (%, %) -> Boolean
<: (%, %) -> Boolean	[default]
>=: (%, %) -> Boolean	[default]
<=: (%, %) -> Boolean	[default]
max: (%, %) -> %	[default]
min: (%, %) -> % Maximum and minimu argument.	[default]
>: (%, %) -> Cross(Boolean, %) Greater than test.	[default]
<: (%, %) -> Cross(Boolean, %) Less tahn test.	[default]
>=: (%, %) -> Cross(Boolean, %) Greater tahn or equal test.	[default]
<=: (%, %) -> Cross(Boolean, %) Less than or equal test.	[default]
>: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default]
<: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default]
>=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default]
<=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default]
>: (Cross(Boolean, %), %) -> Boolean	[default]
<: (Cross(Boolean, %), %) -> Boolean	[default]
>=: (Cross(Boolean, %), %) -> Boolean	[default]
<=: (Cross(Boolean, %), %) -> Boolean	[default]
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> TextWriter	from BasicType

Definition:

define Order: Category == BasicType with {
        >:      (%, %) -> Boolean;
        <:      (%, %) -> Boolean;
        >=:     (%, %) -> Boolean
        <=:     (%, %) -> Boolean
        max:    (%, %) -> %
        min:    (%, %) -> %

       default {
               (x: %) <  (y: %): Bolean == y > x;
               (x: %) >= (y: %): not (x < y);
               (x: %) >= (y: %): not (x > y);
               max(x: %, y: %): % == if x > y then x else y;
               min(x: %, y: %): % == if x < y then x else y;
}

default {
               -- These allow sequences, /eg{}:   0 <= i < n;
               B% ==> Cross(Boolean, %);

               (x: %)   >  (y: %): B%      == (x >  y, y);
               (x: %)   <  (y: %): B%      == (x <  y, y);
               (x: %)   >= (y: %): B%      == (x >= y, y);
               (x: %)   <= (y: %): B%      == (x <= y, y);

               (bx: B%) >  (y: %): B%      == {(b,x) := bx;
                                              (b and x >  y, y)}
               (bx: B%) <  (y: %): B%      == {(b,x) := bx;
                                              (b and x <  y, y)}
               (bx: B%) >= (y: %): B%      == {(b,x) := bx;
                                              (b and x >= y, y)}
               (bx: B%) <= (y: %): B%      == {(b,x) := bx;
                                              (b and x <= y, y)}

               (bx: B%) >  (y: %): Boolean == {(b,x):=bx; b and x >  y}
               (bx: B%) <  (y: %): Boolean == {(b,x):=bx; b and x <  y}
               (bx: B%) >= (y: %): Boolean == {(b,x):=bx; b and x >= y}
               (bx: B%) <= (y: %): Boolean == {(b,x):=bx; b and x <= y}
        }
}

25.23 : OrderedAbelianGroup

Description:
`OrderedAbelianGroup' provides group operations consitent with an order.

Directly inherits:
OrderedAbelianMonoid, AbelianGroup

Exports:

=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> TextWriter	from BasicType
<, >, <=, >=: (%, %) -> Boolean	from Order
<, >, <=, >=: (%, %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Boolean	[default] from Order
min, max: (%, %) -> %	[default] from Order
0: %	from AbelianMonoid
+: % -> %	[default from AbelianMonoid
+: (%, %) -> %	from AbelianMonoid
zero?: % -> Boolean	[default] from AbelianMonoid
-: % -> %	from AbelianGroup
-: (%, %) -> %	[default] from AbelianGroup

Definition:

define OrderedAbelianGroup: Category ==
        Jon(OrderedAbelianMonoid, AbelianGroup);

25.24 : OrderedAbelianMonoid

Description:
`OrderedAbelianMonoid' provides an addition consitent with an order.

Directly inherits:
Order, AbelianMonoid

Exports:

=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> TextWriter	from BasicType
<, >, <=, >=: (%, %) -> Boolean	from Order
<, >, <=, >=: (%, %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Boolean	[default] from Order
min, max: (%, %) -> %	[default] from Order
0: %	from AbelianMonoid
+: % -> %	[default from AbelianMonoid
+: (%, %) -> %	from AbelianMonoid
zero?: % -> Boolean	[default] from AbelianMonoid

Definition:

define OrderedAbelianMonoid: Category == Join(Order, AbelianMonoid);

25.25 : OrderedFinite

Description:
`OrderedFinite' provides the minimum and maximum valoues for a finite type.

Directly inherits:
Finite, Order

Exports:

min: %
max: % Minimum and maximum value belonging to the type
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> TextWriter	from BasicType
#: Integer	from Finite
<, >, <=, >=: (%, %) -> Boolean	from Order
<, >, <=, >=: (%, %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Boolean	[default] from Order
min, max: (%, %) -> %	[default] from Order

Definition:

define OrderedFinite: Category == Join(Finite, Order) with {
        min: %;
        max: %;
}

25.26 : OrderedRing

Description:
`OrderedRing' provides arithmetic consitent with an ordering.

Directly inherits:
OrderedAbelianGroup, Ring

Exports:

abs: % -> % Absolute value.	[default]
sign: % -> % -1, 0 or 1.	[default]
negative?: % -> Boolean Test whether value is negative.	[default]
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) => TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
<, >, <=, >=: (%, %) -> Boolean	from Order
<, >, <=, >=: (%, %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Boolean	[default] from Order
min, max: (%, %) -> %	[default] from Order
0: %	from AbelianMonoid
+: % -> %	[default from AbelianMonoid
+: (%, %) -> %	from AbelianMonoid
zero?: % -> Boolean	[default] from AbelianMonoid
-: % -> %	from AbelianGroup
-: (%, %) -> %	[default] from AbelianGroup
1: %	from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem

Definition:

define Orderedring: Category == Join(OrderedAbelianGroup, Ring) with {
        abs:       % -> %;
        sign:      % -> %;
        negative?: % -> Boolean;
        positive?: % -> Boolean;
        
        default {
                abs (x: %): % == if x > 0 then x else -x;
                sign(x: %): % == {x > 0 => 1; x < 0 => -1; 0}
                negative?(x: %) : Boolean == x < 0;
                positive?(x: %) : Boolean == x > 0;
        }
}

25.27 : Ring

Description:
`Ring' provides the basic arithmetic operations of addition, subtraction and multiplication.

Directly inherits:
Arithmeticsystem, Monoid, AbelianGroup

Exports:

0: %	from ArithmeticSystem
+: % -> %	[default] from ArithmeticSystem
+: (%, %) -> %	from ArithmeticSystem
-: % -> %	from ArithmeticSystem
-: (%, %) -> %	[default] from ArithmeticSystem
1: %	from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem
coerce: SingleInteger -> %	from ArithmeticSystem
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) -> TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	[default] from BasicType
hash: % -> SingleInteger	[default] from BasicType
zero?: % -> Boolean	[default] from AbelianMonoid

Definition:

define Ring: Category == Join(ArithmeticSystem, Monoid, AbelianGroup);

25.28 : Steppable

Description:
`Steppable' provides skuposrt for segments: discrete sets of values hwich can be stepped over in order.

Directly inherits
OrderedRing

Exports:

stepsBetween: (%, %, %) -> SingleInteger `stepsBetween(a,b,n)' returns the number os steps between a and b at intervals of n.
stepsBetween `stepsBetween(a,b)' returns the number of steps between a and b	[default]
=: (%, %) -> Boolean	from BasicType
~=: (%, %) -> Boolean	[default] from BasicType
<<: (TextWriter, %) => TextWriter	from BasicType
<<: % -> TextWriter -> TextWriter	[default] from BasicType
sample: %	from BasicType
hash: % -> SingleInteger	[default] from BasicType
<, >, <=, >=: (%, %) -> Boolean	from Order
<, >, <=, >=: (%, %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Cross(Boolean, %)	[default] from Order
<, >, <=, >=: (Cross(Boolean, %), %) -> Boolean	[default] from Order
min, max: (%, %) -> %	[default] from Order
0: %	from AbelianMonoid
+: % -> %	[default from AbelianMonoid
+: (%, %) -> %	from AbelianMonoid
zero?: % -> Boolean	[default] from AbelianMonoid
-: % -> %	from AbelianGroup
-: (%, %) -> %	[default] from AbelianGroup
1: %	from ArithmeticSystem
*: (%, %) -> %	from ArithmeticSystem
^: (%, Integer) -> %	from ArithmeticSystem
coerce: Integer -> %	from ArithmeticSystem
abs: %-> %	[default] from OrderedRing
sign: % -> %	[default] from OrderedRing
negative?: % -> Boolean	[default] from OrderedRing
positive?: % -> Boolean	[default] from OrderedRing

Definition:

define Steppable: Category == OrderedRing with {
        stepsBetween: (%, %, %) -> SingleInteger;
        stepsBetween: (%,%) -> SingleInteger;
        default stepsBetween(x: %, y: %): SingleInteger == {
                    stepsBetween(x, y, 1);
        }
}