Functions lie at the heart of Aldor:
typical expressions consist mostly of function calls.
Much of what is done by ad hoc means in other languages
is done in Aldor through normal functions.
It is the job of the compiler to ensure that relying on functions
in this way does not adversely affect performance.
This chapter describes how to define and use functions, beginning with
typical examples of function definition and application, then describing
more specialized features, including keyword arguments, default
arguments, function expressions (also called ``anonymous functions''),
and curried functions.
6.1 : Function definition
A typical function definition has the following form:
f (s1: S1, ..., sn: Sn) : T == E
This definition has a number of parts:
- the function name, f
- the formal parameter names, s1,...,sn
- the formal parameter types, S1,...,Sn
- the return type, T, and
- the function body, E.
The function name is an identifier which will be used
to denote the function.
In a given scope there may be more than one functions with the same
name; in this case the function name is said to be overloaded.
The formal parameter names are identifiers which are used to
refer to the values passed to the function as arguments. The formal
parameter names are visible in the body of the function, in the types
of the formal parameters, and in the return type (See
section 8.12).
The formal parameter types are type-valued expressions
(e.g. "Integer" or "SquareMatrix(n+m, Complex Float)")
which specify what type of value is expected as the corresponding
actual argument to the function.
The return type is a type-valued expression which specifies
the type of the value computed by the function.
The function body is an expression which, when evaluated,
produces the return value of the function. The type of the
value returned by the function body must be compatible
with the given return type.
More elaborate forms of function definitions are described in section 6.6;
Multiple return values
Just as functions can take any number of parameters, they may also
return any number of results. The typical function definition given above
is a special case of the more general form:
f (s1: S1, ..., sn: Sn) : (t1: T1, ..., tm: Tm) == E
Now in place of a single return type we have:
- the return names, t1,...,tm, and
- the return types, T1,...,Tm.
This function definition takes n arguments and returns m results.
The return names are identifiers which can be used
to refer to the values returned from the function.
The return names are visible in the types of the return values.
The return types are type-valued expressions which specify
the type of the corresponding value returned from the function.
Any or all of the return names may be omitted,
in which case the ith return declaration would read "Ti",
rather than "ti: Ti".
When a function has no formal parameter or no return value
an empty pair of parentheses is used as the formal parameter list
or return value list.
For example, the following function takes no parameter and
returns no result:
f () : () == E
Return expressions
Inside the body of a function definition, a return expression is used
to explicitly pass control back to the calling environment and to return
values from the function. The general form of the return expression is:
return E
The value of the expression "E" is returned as the value
of the function. The type of "E" must be compatible with
the declared return type of the function. The return expression
itself has type "Exit".
Inside a function which returns more than one value the return expression
may explicitly supply more than one value:
return (v1, ..., vn)
Inside a function which returns no value, an empty return expression
may be used:
return
Since the value of the function body is used as the value of the function,
in many cases an explicit return expression is unnecessary:
f (n: Integer) : Integer == if n < 1 then 1 else n * f(n-1)
The value returned by the function "f" is the value returned by
the "if" expression. An explicit "return" is not needed.
6.2 : Function application
A typical (prefix) function application has the following form:
f (a1, ..., an)
This form of function application has the following parts:
- the function, f, and
- the actual parameters, a1,...,an.
The function is an expression which denotes the function to be called.
In general, f can be any expression whose value is a function.
The actual parameters are expressions which specify the values
to be passed as arguments to the function. The types of the actual
parameters must be compatible with the type of the function f.
As discussed in section 5.8, the order of evaluation
of the actual arguments in an application is not defined. More elaborate
forms of function application are developed in section 6.3, section 6.5 and section 6.6.
When a function takes no parameter, an application of that
function must have as its actual parameters an expression which produces
no value. Often, such an application takes the following form:
f ()
Other application notations
In addition to the normal prefix application notation there are a
small number of special syntactic forms in Aldor denoting function
application. The general reason behind these rules is to make
programs more readable. For example there is a set of infix operators
(see section 4.4), so that you can write a +
b instead of +(a,b). Futhermore, some language forms cause
implicit application of functions:
- the treatment of literal values,
- the application of one object to another,
- the updating of objects,
- the interpretation of tests in conditional statements
- the mechanism for generating a set of values for iteration.
Refer to chapter 11 for a more detailed description of these forms.
6.3 : Keyword arguments
Consider the following function definition:
-- Compute a point on the line with slope `m' and intercept `b'.
line(x: Float, m: Float, b: Float): Float == m*x + b;
Because all the parameters have the same type, it may be difficult
to remember which one is which. As a result, the meaning of a call such as
line(3.2, 8.2, 1.0);
might not be readily apparent.
One way to increase the readability of such a program is to place
the arguments in named variables before calling the function:
slope := 8.2;
intercept := 1.0;
line(3.2, slope, intercept);
But this approach needlessly increases the number of variables
used by the program. In addition, now the values for the slope
and intercept are not explicitly visible at the call point.
So one sort of unreadability has been exchanged for another
(and remembering the order of the parameters is no easier
than before).
Keyword arguments
An alternative in Aldor is to allow the actual arguments
in an application to be supplied by name using keyword arguments.
For example:
line(3.2, b == 1.0, m == 8.2);
An actual argument in this form of application has the following parts:
- the formal parameter name, (e.g. b),
- the double-equal symbol "==" and
- the actual parameter value, (e.g. 1.0).
The formal parameter name is an identifier which must match
one of the formal parameter names given in the definition of the function.
The actual parameter value is then used as the value of the formal
parameter with the same name, regardless of its position in the actual
argument list in the function application. The type of the actual parameter
value must match the type of the formal parameter with the same name.
Any parameters supplied as keyword arguments must appear after any arguments
supplied by position alone. It is an error if any of the formal parameters
is not supplied with a value, either as a positional argument or by using
a keyword argument.
6.4 : Default arguments
In a programming language where function names may not be overloaded,
such as Lisp or C, some functions are written to take a variable number
of arguments. When these functions are called, they decide which arguments
they have been passed and what to do about the missing ones.
In a language such as Aldor, where function names may be overloaded,
there are often several functions visible with the same name.
Which function to use is decided on the basis of the number of actual arguments
supplied and their types, and possibly on the type of the return value
required by the context of the function application.
So, instead of writing functions which take a variable number of
arguments, in Aldor we are allowed to write several functions with
with same name, each with a fixed number of arguments. One advantage
of doing this is that the decision on which function to call can be made
once, at compile time, whereas code in the body of the function, to
supply missing arguments, would be exercised in each time the function
was run.
So, continuing the example from section 6.3, we can write:
-- Compute a point on the line with slope `m' and intercept `b'.
line(x: Float, m: Float, b: Float): Float == m*x + b;
-- Assume a default intercept of `0'.
line(x: Float, m: Float): Float == line(x, m, 0);
Soon afterward, however, we want to give other arguments default values.
Then the number of functions needed increases exponentially in the number
of arguments which are to have default values.
Another problem arises when arguments have the same type:
it is not always possible to overload the function name enough to
provide each argument with a default value.
For these reasons, languages with name overloading sometimes provide
an explicit way to supply default values to named parameters.
Default arguments
In Aldor, default values for named parameters can be supplied in
the definition of a function using the following form:
f (s1: S1 == v1, ..., sn: Sn == vn) : T == E
This form of function definition has the following additional part:
- the default argument value specifications, in which
"==" (the double-equal symbol) introduces each of the
default argument values, v1,...,vn.
The default argument values are expressions which, when evaluated,
produce values, each of which can be used as the corresponding argument
to the function. The type of the default value for a parameter must be
compatible with the corresponding parameter type.
Any or all of the default argument values may be omitted, in which case the
form of the ith formal parameter would read "si: Si" instead of
"si: Si == vi". A function definition which supplies a default argument
value for one of its parameters must also supply a default argument
value for each of the following parameters.
Once again continuing the example given above, we can now define a single
function which allows any combination of its final two arguments to be omitted:
-- Compute a point on the line with slope `m' and intercept `b'.
-- The default slope is 1, and the default intercept is 0.
line(x: Float, m: Float == 1, b: Float == 0) : Float == m*x + b;
This definition supplies a default value of 1 for "m",
and a default value of 0 for "b". Some example
applications of the function "line" are as follows:
x: Float := 3.2;
print << line(x, 8.0) << newline; -- 8.0 * x + 0
print << line(x) << newline; -- 1 * x + 0
print << line(x, b == 5.0) << newline; -- 1 * x + 5.0
In an application of a function whose definition supplies default
argument values, it is an error if any of the formal parameters is not
supplied with a value, either as a positional argument, or by using a
keyword argument, or by using the default argument value supplied (if
any) for that formal parameter. The default argument values are
evaluated, if and when they are used in a function application, as the
other actual parameters are evaluated. As discussed in
section 5.8 the order of evaluation of the actual
arguments to an application is not defined.
6.5 : Function expressions
Function expressions are the primitive form for building functions
in Aldor. The general form for a function expression is:
(s1: S1 == v1, ..., sn: Sn == vn) : (t1: T1, ..., tm: Tm) +-> E
The syntax "(s: S) : T +-> E(s)" for a function expression
is intended to resemble the mathematical notation 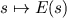 for a function specification. The infix keyword +-> denotes the
for a function specification. The infix keyword +-> denotes the 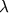 operator from a typed lambda calculus.
A function expression has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types,
the function body (see section section 6.1), and
default arguments (see section 6.4).
operator from a typed lambda calculus.
A function expression has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types,
the function body (see section section 6.1), and
default arguments (see section 6.4).
When a function expression is evaluated, it captures the lexical environment
in which it appears, creating a lexical closure. The values of the variables
which are visible in the scope of the function expression are then available
when it is eventually applied to a set of arguments.
More typical cases of function expressions are formed in much the same
way as the corresponding cases of function definitions. For example,
the expression:
(f: Integer -> Integer, n: Integer) : Integer +->
if n < 1 then 1 else n * f(n-1)
represents an integer function of two arguments which bears some superficial
resemblance to a factorial function.
Since a function expression has the same parts as a function
definition except for the name, function expressions are sometimes
known as anonymous functions. Function expressions are also known as lambda
expressions in many programming languages.
Function types
Like any other expression, a function expression can be assigned a type.
The type assigned to a function expression is called a function type.
A function type is formed with the infix keyword "->":
(s1: S1 == v1, ..., sn: Sn == vn) -> (t1: T1, ..., tm: Tm)
The syntax "S -> T" for a function type is intended to be reminiscent
of the mathematical notation 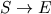 for a set of functions.
A function type has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types
(see section 6.1), and default arguments
(see section 6.4).
for a set of functions.
A function type has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types
(see section 6.1), and default arguments
(see section 6.4).
For function types, any or all of the formal parameter names may be omitted,
in which case the ith parameter declaration would read "Si"
rather than (in the most general case) "si: Si == vi".
The type of "f", "(Integer -> Integer)", in the function
expression shown previously, is a typical example of a function type.
Any function expression which takes one integer argument and returns
one integer result is a member of this type.
The ability to include the formal parameter names and default arguments
in the specification of the type is useful when using
keyword arguments (see section 6.3),
default arguments (see section 6.4), and
dependent types (see section 13.2).
Function definition revisited
The typical form for a function definition given in
section 6.1is really just a shorthand
for the following equivalent definition:
f : (s1: S1, ..., sn: Sn) -> T == (s1: S1, ..., sn: Sn) : T +-> E
This form makes it easier to see that the function defintions are the same as defintions of any other values. Specifically, the expression:
n : Integer == 8
defines a type ("Integer") and a value ("8") for the identifier
"n". In the same way the function definition:
f (n: Integer) : Integer == if n < 1 then 1 else n * f(n-1)
which can also be written as:
f : (n: Integer) -> Integer ==
(n: Integer) : Integer +-> if n < 1 then 1 else n * f(n-1)
defines a function type ("(n: Integer) -> Integer") and
a function expression for the identifier "f".
Function application revisited
Since function expressions evaluate to functions, they can be used
in the place of the function name in a function application:
((n: Integer) : Integer +-> if n < 1 then 1 else n * (n-1))(5);
This way of calling function expressions may be rather verbose. However,
function expressions can also be assigned to local variables:
g := (n: Integer) : Integer +-> if n < 1 then 1 else n * (n-1);
g(5);
So once again we see that a typical function definition is merely
a special case of a more general framework, based on the fact that
function expressions can be used just like any other expression.
6.6 : Curried functions
Since function expressions can be used just like any other
expression, we can write a function which returns a function as its result:
line (m: Float, b: Float) : (x: Float) -> Float ==
(x: Float) : Float +-> m*x + b
The function line is a function which has two formal parameters,
and which returns a function of one formal parameter. The type of the
function returned by line is (x: Float) -> Float.
A function which returns a function as its result is called
a curried function,
after Haskell Curry, a significant contributor to the theory behind
functional programming.
To simplify the definition of curried functions in Aldor,
two shorthand notations are provided.
Function expressions revisited
First, we generalize the syntax of function expressions
(see section 6.5) by inductively defining
the curried function expression
(s1: S1) ... (sn: Sn)(s0: S0) : T +-> E
to be equivalent to the expression
(s1: S1) ... (sn: Sn) : (s0: S0) -> T +-> (s0: S0) : T +-> E
In the definition above, we have assumed a single formal parameter within
each set of parentheses and a single return type, to simplify the exposition.
Note that "->"; and "+->" associate from right to left
and that "->" groups more tightly than "+->".
Using the equivalent method of writing function definitions, given in
section 6.5, and applying this shorthand to the
right-hand side, the definition of the function line given above
can be written as:
line : (m: Float, b: Float) -> (x: Float) -> Float ==
(m: Float, b: Float)(x: Float) : Float +-> m*x + b
Note that the function line is still a function which has
two formal parameters, and which returns a function of one formal parameter.
The only additional notation used here is the curried function expression
used to define the value of line. An expression for line can
be written without using a curried function expression, but the shorter form
is more convenient.
Function definition revisited
As a second shorthand for defining curried functions, we define
the curried function definition
f (s1: S1) ... (sn: Sn) : T == E
to be equivalent to the expression
f : (s1: S1) -> ... -> (sn: Sn) -> T ==
(s1: S1) ... (sn: Sn) : T +-> E
Continuing the example from the previous paragraphs, we can now express
the definition of the function line in its most convenient form:
line (m: Float, b: Float)(x: Float) : Float == m*x + b
As a further example, if we define exponentiation for SingleInteger functions
of a SingleInteger as follows:
S ==> SingleInteger;
(f:(S->S))^(n:S) : (S->S) == {
n = 0 => (x:S):S +-> x;
n = 1 => f;
(x:S):S +-> f((f^(n-1))x);
}
an alternative notation could be defined, using the curried function
conventions, as:
multApply(n:S,f:(S->S)):S->S == f^n
Function application revisited
The application of curried functions to their arguments needs no additional
machinery: a curried function is just a function which returns a function,
and any expression (including the result of a function application) can be
used as a function as long as the actual parameters to the application are
compatible with the type of the function. For example:
#include "aldor"
import from Float;
line(m: Float, b: Float)(x: Float): Float == m*x + b;
print << "f(x) is x - 1" << newline;
print << "f(1.0) = " << line(1,-1)(1.0) << newline;
print << "f(2.0) = " << line(1,-1)(2.0) << newline;
print << "f(3.0) = " << line(1,-1)(3.0) << newline;
So in the application line(1,-1)(1.0), the curried function line
is applied to the arguments 1 and -1, which returns a function
of one argument, which is applied to the argument 1.0.
As a result, we can use the line function in this example
to create other functions:
#include "aldor"
import from Float;
line(m: Float, b: Float)(x: Float): Float == m*x + b;
f := line(1, -1);
print << "f(x) is x - 1" << newline;
print << "f(1.0) = " << f(1.0) << newline;
print << "f(2.0) = " << f(2.0) << newline;
print << "f(3.0) = " << f(3.0) << newline;
When we supply in this way only some of the arguments to a function,
the result is a new function related to the original.
This technique is a basic feature of functional programming,
and is known as currying a function.
Some languages provide an automatic conversion of functions of
type (A, B) -> C to functions of type A -> B -> C.
This automatic conversion is not done in Aldor.
When desired, this conversion can be made explicitly with a
function expression:
#include "aldor"
import from Integer;
I ==> Integer;
-- Curry the function `*'
ctimes == (a: I)(b: I) : I +-> a * b;
times3 == ctimes 3
print << "3 * 2 = " << times3 2 << newline;
-- Convert general functions:
curry(f: (I, I) -> I)(a: I)(b: I) : I == f(a,b);
print << "3 + 2 = " << curry(+)(3)(2) << newline;
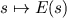 for a function specification. The infix keyword +-> denotes the
for a function specification. The infix keyword +-> denotes the 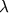 operator from a typed lambda calculus.
A function expression has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types,
the function body (see section section 6.1), and
default arguments (see section 6.4).
operator from a typed lambda calculus.
A function expression has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types,
the function body (see section section 6.1), and
default arguments (see section 6.4). Previous
Previous
 Home
Home
 Contents
Contents
 Next
Next
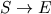 for a set of functions.
A function type has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types
(see
for a set of functions.
A function type has many of the same parts as a function definition,
including the formal parameter names/types, the return names/types
(see